We explained previously that the degree of belief in an uncertain event A was conditional on a body of knowledge K. Thus, the basic expressions about uncertainty in Bayesian approach are statements about conditional probabilities. This is why we used the notation P(A|K) which should only be simplified to P(A) if K is constant.

In general we write P(A|B) to represent a belief in A under the assumption that B is known. Even this is, strictly speaking, shorthand for the expression P(A|B,K) where K represents all other relevant information. Only when all such other information is irrelevant can we really write P(A|B).

The traditional approach to defining conditional probabilities is via joint probabilities. Specifically we have the well known ‘formula’:

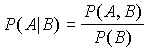
This should be really thought of as an axiom of probability. Just as we saw the three probability axioms were ‘true’ for the frequentist approach, so this axiom can be similarly justified in terms of frequencies:

Example: Let A denote the event ‘student is female’ and let B denote the event ‘student is Chinese’. In a class of 100 students suppose 40 are Chinese, and suppose that 10 of the Chinese students are females. Then clearly, if P stands for the frequency interpretation of probability we have:

P(A,B) = 10/100 (10 out of 100 students are both Chinese and female)

P(B) = 40/100 (40 out of the 100 students are Chinese)

P(A|B) = 10/40 (10 out of the 40 Chinese students are female)

It follows that the formula for conditional probability ‘holds’.

In those cases where P(A|B) = P(A) we say that A and B are independent.
If P(A|B,C) = P(A|C) we say that A and B are conditionally independent given C.