In the classic simple Bayesian problem we have:
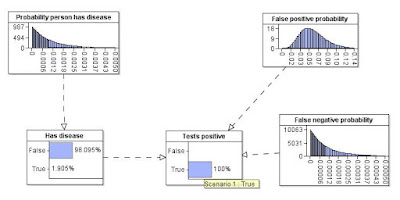
- a hypothesis H (such as ‘person has specific disease’) with a prior probability (say 1 in a 1000) and
- evidence E (such as a test result which may be positive or negative for the disease) for which we know the probability E given H (for example the probability of a false positive is 5% and the probability of a false negative is 0%).
With those particular values Bayes’ theorem tells us that a randomly selected person who tests positive has a 1.96% probability of having the disease.
But what if there is uncertainty about the prior probabilities (i.e. the 1 in a 1000, the 5% and 0%). Maybe the 5% means ‘anywhere between 0 and 10%’. Maybe the 1 in a 1000 means we only saw it once in 1000 people. This new technical report explains how to properly incorporate uncertainty about the priors using a Bayesian Network.





Recent Comments